Termin (modul) u doslovnom prijevodu sa latinskog znači "zahíd". Koncept je u matematiku uveo engleski naučnik R. Kotes. A njemački matematičar K. Wejerstrass, nakon što je saznao za znak modula, je simbol, što znači da je sat pisanja namijenjen za razumijevanje.

U kontaktu sa

Prije svega, razumiješ matematiku za program 6. razreda srednje škole. Zgídno s jednim íz vyznachen, modulo - tse apsolutna vrijednost broja. Drugim riječima, da bi se prepoznao modul decimalnog broja, potrebno je odabrati njegov predznak.

Grafički apsolutna vrijednost ali yak |a|.

Glavna ideja riže se razumije činjenicom da je vino nenegativna vrijednost.

Brojevi, koji izgledaju kao jedan te isti kao znak, nazivaju se suprotnosti. Ako je vrijednost pozitivna, suprotna vrijednost će biti negativna, a nula će biti suprotna samoj sebi.

geometrijska vrijednost

Da bi se koncept modula shvatio sa pozicije geometrije, smisleno je sagledati ga, moguće ga je napraviti u pojedinačnim redovima od klipa koordinata do zadate tačke. Svrha oznake je proširiti geometrijski smisao posljednjeg pojma.

Grafički, možete to reći ovako: |a| = O.A.

Moć apsolutne vrijednosti

U nastavku će biti prikazane sve matematičke moći ovog razumijevanja i način na koji se zapisuju slova riječi:

Karakteristike

Kada se govori o razvoju matematičkih jednakosti i nedosljednosti, koje imaju modul, potrebno je zapamtiti da je njihovo izražavanje neophodno za prepoznavanje znaka.

Na primjer, kao znak apsolutne vrijednosti, za oduzimanje određene matematičke viraze, prije nje, kao modula, potrebno je osigurati fiktivnu matematičku oznaku.

|A + 5| = A + 5, yakscho, A više ili više jednako je nuli.

5-A ako je A manje od nule.

U nekim vipadkama, znak se može nedvosmisleno razviti za bilo koji znak promjene.

Pogledajmo još jedan primjer. Razmotrimo koordinatnu liniju koja označava sve numeričke vrijednosti čija će apsolutna vrijednost biti 5.

Za klip je potrebno preći koordinatnu liniju, zadati joj koordinate i podesiti veličinu jednog klina. Uz to, majka je direktno kriva. Sada je na ovoj pravoj liniji potrebno nanijeti rozete, kako bi se prilagodila veličina jednog namotaja.

Ovim redoslijedom možemo reći da će na koordinatnoj liniji biti dvije tačke koje će nas označiti, sa vrijednostima 5 i -5.

Jedna od najzanimljivijih tema za uchnív je rozvyazannya rivnyan, scho da osveti promjenu pod znakom modula. Hajde da pogledamo klip, zašto je vezan? Zašto, na primjer, kvadratni jednaki više djece zveckaju kao grašak, a sa tako daleko od najboljeg razumijevanja, poput modula, može li biti više problema?

Po mom mišljenju, svi nabori su zbog postojanja jasno formulisanih pravila za implementaciju modula. Dakle, virishyuyuchi kvadrat jednak, učenici tačno znaju šta vam je potrebno da zapišete formulu diskriminanta, a zatim i formulu korijena kvadrata jednakog. A šta je sa robotom, kako bi bilo da modul bude fiksiran na jednakom tlu? Pokušat ćemo jasno opisati potreban plan za to vrijeme, ako je jednak osveti nepoznatom pod znakom modula. Donijet ćemo papalinu aplikacija na kapi kože.

Pivo za klip oznaka modula. Otac, modul broja a zvao isti broj, kao a Ne vidim -a, što je broj a manje od nule. Možete to napisati ovako:

|a| = a ako je a ≥ 0 i |a| = -a, isto što i a< 0

Govoreći o geometrijskom smislu modula, sljedeća stvar koju treba zapamtiti je da decimalni broj kože ima jednu tačku na numeričkoj osi - í̈ do koordinata. Dakle, osa, modul ili apsolutna vrijednost broja, naziva se udaljenost od centra tačke do klipa u numeričkoj osi. Uvijek dobijete pozitivan broj. U ovom redoslijedu, modul bilo kojeg negativnog broja je pozitivan. Prije govora naučite u kojoj fazi mnogi učenici počinju da zalutaju. Modul može imati broj, a rezultat unosa modula je uvijek pozitivan broj.

A sada idemo dalje bez problema do otvora rijeke.

1. Perspektiva jednaka umu | \u003d s, de s - deisne broj. Cijena se može provjeriti uz pomoć modula.

Svi trenutni brojevi su podeljeni u tri grupe: tí, koji je veći od nule, tí, koji je manji od nule, i treća grupa je ceo broj 0. Zapišimo rešenje za vizuelnu šemu:

(±c, ako je s > 0

Yakscho | x | = c, tada je x = (0, dakle c = 0

(bez korijena, yakscho z< 0

1) | = 5, jer 5> 0, tada je x = ±5;

2) | = -5 jer -pet< 0, то уравнение не имеет корней;

3) | = 0 onda je x = 0.

2. Jednako umu | f(x) | = b de b > 0. Da biste dovršili ovo poravnanje, morate dobiti modul. Robimo tse: f(x) = b chi f(x) = -b. Sada je potrebno popraviti kožu od otrimanih jednakih. Yakshcho za vikend Rivnian b< 0, решений не будет.

1) | x + 2 | = 4, jer 4 > 0, onda

x + 2 = 4 ili x + 2 = -4

2) | x 2 - 5 | = 11, jer 11 > 0, onda

x 2 - 5 = 11 ili x 2 - 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 bez korijena

3) | x 2 - 5x | = -8, jer -8< 0, то уравнение не имеет корней.

3. Rivnyannya um | f(x) | = g(x). Za zamjenu modula, takvo rješenje je jednako majci, na primjer, dio zakona je veći od nule, tobto. g(x) ≥ 0. Tada možemo izračunati:

f(x) = g(x) ili f(x) = -g(x).

1) | 2x - 1 | \u003d 5x - 10. Trošak matima je korijen, yakscho 5x - 10 ≥ 0. Sam početak rozvyazannya takvih rivna.

1. O.D.Z. 5x – 10 ≥ 0

2. Rješenja:

2x - 1 = 5x - 10 ili 2x - 1 = - (5x - 10)

3. Kombinirani O.D.Z. tu odluku donosimo:

Koren x = 11/7 nije pogodan za O.D.Z., vin je manji od 2, a x = 3 je zadovoljstvo vašeg uma.

Prijedlog: x = 3

2) | x - 1 | = 1 - x 2.

1. O.D.Z. 1 – x 2 ≥ 0

(1 – x)(1 + x) ≥ 0

2. Rješenja:

x - 1 = 1 - x 2 ili x - 1 = - (1 - x 2)

x 2 + x - 2 = 0 x 2 - x = 0

x = -2 ili x = 1 x = 0 ili x = 1

3. Zajednička odluka i O.D.Z.:

Više od korijena je pogodno za x = 1 i x = 0.

Prijedlog: x=0, x=1.

4. Jednako umu | f(x) | = | g(x)|. Ovo je jednako dvije nadolazeće jednakosti f(x) = g(x) ili f(x) = -g(x).

1) | x 2 - 5x + 7 | = | 2x - 5 |. Tse jednako dva će doći:

x 2 - 5x + 7 = 2x - 5 ili x 2 - 5x +7 = -2x + 5

x 2 - 7x + 12 = 0 x 2 - 3x + 2 = 0

x = 3 ili x = 4 x = 2 ili x = 1

Prijedlog: x = 1, x = 2, x = 3, x = 4.

5. Rivnyannya, yakí vyríshuyusya način zamjene (zamijenite promjenu). Dansku metodu rješenja najlakše je objasniti na određenoj primjeni. Dakle, dajmo kvadrat jednak modulu:

x 2 – 6|x| + 5 = 0. Za kvalitet modula x 2 = |x| 2, koji se može prepisati ovako:

|x| 2 - 6 | x | + 5 = 0. Promijenimo | = t ≥ 0, onda matematika:

t 2 - 6t + 5 \u003d 0. Uzimajući u obzir datu jednakost, pretpostavljamo da je t = 1 ili t = 5. Okrenimo se da zamijenimo:

|x| = 1 chi |x| = 5

x = ±1 x = ±5

Prijedlog: x=-5, x=-1, x=1, x=5.

Pogledajmo još jedan primjer:

x 2 + | – 2 = 0. Za kvalitet modula x 2 = |x| 2 , do

|x| 2+ |x| - 2 = 0. Promijenimo | x | = t ≥ 0 onda i:

t 2 + t - 2 \u003d 0. Prilično je jednako, prihvatljivo je, t \u003d -2 ili t \u003d 1. Okrenimo se da zamijenimo:

|x| = -2 chi |x| = 1

Nema korijena x = ± 1

Prijedlog: x=-1, x=1.

6. Druga vrsta poravnanja je poravnanje sa "sklopivim" modulom. Do takvih jednakosti može se vidjeti ekvilizacija, u kojoj postoje moduli u modulima. Rivnyannya tsgogo um može biti narušen, blokirajući snagu modula.

1) |3 – |x|| \u003d 4. D_yatimemo je isti, kao u jednakima drugog tipa. Jer 4 > 0, onda uzimamo dvije jednakosti:

3 - | x | = 4 chi 3 – |x| = -4.

Sada se virazimo na nivou skin modula x, todi | = -1 chi |x| = 7.

Virishuemo kožu od otrimanih jednakih. Prvi jednak nema korijen, jer -jedan< 0, а во втором x = ±7.

Provjerite x=-7, x=7.

2) | 3 + | x + 1 | | = 5

3 + | x + 1 | = 5 chi 3 + |x + 1| = -5

|x + 1| = 2 | x + 1 | = -8

x + 1 = 2 ili x + 1 = -2. Ne postoji root.

Prijedlog: x=-3, x=1.

ísnuê shchey i univerzalna metoda rozv'yazannya ívnyan íz modula. Tse metoda intervala. Ale mi yogo pogledao.

blog.website, sa novom ili privatnom kopijom materijala poslanom na originalnom povezu.

MBOU ZOSh br. 17 m. Ivanova

« Rivnyannya sa modulom "
Metodički razvoj

Zaliha

nastavnik matematike

Lebedeva N.V.

20010

Objašnjenje

Odjeljak 1. Uvod

Odjeljak 2. Glavne ovlasti Odjeljak 3. Geometrijska interpretacija pojma modula broja Odjeljak 4. Grafikon funkcije y = | Odjeljak 5. Mentalna spoznaja

Dio 2

Razdíl 1.Rivnyannya um | F(x) | = m (najlakše) Odjeljak 2. Jednako obliku F(|h|) = m Odjeljak 3. Jednako umu | F(x) | = G(x) Odjeljak 4. Jednako umu | F(x) | = ± F(x) (prelijepo) Odjeljak 5. Jednako umu | F(x) | = | G(x) | Rozdíl 6. Nanesite kravatu nestandardne rivn Odjeljak 7. Jednako umu | F(x) | + | G(x) | = 0 Odjeljak 8. Jednako umu | a 1 x ± 1 | ± |a 2 x ± 2 | ± …|a n x ± y n | = m Odjeljak 9

Poglavlje 3

Odjeljak 1. Trigonometrijsko poravnanje Particija 2. Prikaz poravnanja Odjeljak 3. Logaritamska jednačina Odjeljak 4. Iracionalno usklađivanje Odjeljak 5. Nalog za promociju preklapanja Vidpovidí desno Spisak referenci

Objašnjenje.

Koncept apsolutne vrijednosti (modula) decimalnog broja jedna je od suština njegovih karakteristika. Ovo razumijevanje je možda postalo veoma široko u različitim granama fizičkih, matematičkih i tehničkih nauka. U praksi, za predmet matematike u srednjoj školi, do Programa Ministarstva odbrane Ruske Federacije, više puta se konstatuje shvatanje „apsolutne vrednosti broja“: u 6. razredu, oznaka broja uveden je modul, njegov geometrijski zmist; u 8. razredu se formira razumevanje apsolutne greške; u 11. razredu razumijevanje se čuje u odjeljenju „Korin nkorak." Dosvíd vykladannya pokaêê, shcho uchní često stikayutsya z poteškoćama píd hívíshennya zavdan, scho vmagayut poznavanje datog materijala, a često propuštaju, bez prelaska na vikonannya. Slične zadatke sadrže i tekstovi ispitnih zadataka za 9. i 11. razred. Osim toga, ako se prezentuje maturantima škola VNZ-a, oni su rehabilitovani, i to, uglavnom, čak i manje od školskog programa. Za život u budućnosti još je važnije oblikovati matematički stil razmišljanja, koji se manifestuje u pjevanju Rozumovih pridošlica. U procesu izvršavanja zadatka modula, potrebno je zastosovuvati takvu odluku, kao dalju specifikaciju, analizu, klasifikaciju i sistematizaciju, analogiju. Svestranost sličnih zadataka omogućava vam da preispitate poznavanje glavnih podjela školskog kursa, rascjepa logičkog mišljenja i početaka osnovne aktivnosti. Tsya robot je dodijeljen jednom od odjeljenja - virishennya rivnyan, scho da osveti modul. Pobjeda se sastoji od tri divizije. U prvom dijelu uvode se glavni pojmovi i najvažniji teorijski pojmovi. Na drugom je prikazano devet glavnih tipova izjednačavanja, za osvetu modula, sagledani su načini njihovog usavršavanja, pokupljeni su kundaci različitih jednakosti savijanja. Treći ima preklopno i nestandardno poravnanje (trigonometrijsko, displej, logaritamsko i iracionalno). Do dermalnog tipa ispravan je za samostalnu varijantu (date su razne indikacije i uputstva). Osnovna svrha ovog rada je pružanje metodičke pomoći studentima u pripremi za nastavu i u organizaciji fakultativnih predmeta. Materijal se može koristiti i kao vodič za srednjoškolce. Menadžer, ohrabren u radu, cici i ne počni jednostavno od vrha, što vam omogućava da svesnije povećate početnu motivaciju studenata, promenite svoje zdravlje, unapredite obuku diplomiranih studenata do ulaska u VNZ. Diferencijacija prava na promicanje prava na prenošenje prelaska sa reproduktivnog nivoa na materijalni na stvaralački, i na podsticanje sposobnosti učenja za razvijanje znanja o času izvršavanja nestandardnih zadataka.

Odjeljak 1. Uvod.

Odjeljak 1. Imenovanje apsolutne vrijednosti .

Imenovanje : Apsolutna vrijednost (modul) decimalnog broja ali pozvao nepoznati broj: ali ili -ALI. Oznaka: │ ali │ Unos glasi ovako: “modul broja a” ili “apsolutna vrijednost broja a”

│ i ako je a > 0

│a│ = │ 0, dakle a = 0 (1)

│ - a, kao a
Prijavite se: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Proširite Virazu modul:

a) │x - 8│, ako je x > 12 b) │2x + 3│, ako je x ≤ -2 │x - 8│= x - 8 │ 2x + 3│= - 2x - 3

Odjeljak 2. Glavne karakteristike.

Pogledajmo glavnu moć apsolutne veličine. Snaga #1: Protilezhní broj mayut jednakih modula, tobto. │a│=│-a│ Pokažimo vjernost ljubomore. Hajde da zapišemo broj - ali : │- a│= (2) Ravnopravni brakovi (1) i (2). Očigledno je da je oznaka apsolutnih vrijednosti brojeva aliі - ali bježi. otzhe, │a│=│-a│
Gledajući autoritete koji napreduju, miješamo njihove formule, tako da se u njima može pronaći njihov dokaz Snaga #2: Apsolutna vrijednost zbira konačnog broja stvarnih brojeva ne prelazi zbir apsolutnih vrijednosti dodatnih brojeva: Snaga #3: Apsolutna vrijednost razlike između dva realna broja ne prelazi zbir njihovih apsolutnih vrijednosti: │a - v│ ≤│a│+│v│ Snaga #4: Apsolutna vrijednost stvaranja krajnjeg broja realnih brojeva važnija je za završetak apsolutnih vrijednosti množitelja: Snaga #5: Apsolutna vrijednost dijela realnih brojeva jednaka je privatnoj od njihovih apsolutnih vrijednosti:

Odjeljak 3. Geometrijska interpretacija pojma modula broja.

Možete staviti tačku na numeričku liniju za broj kože, kao da je to geometrijska slika broja. Tačka kože na numeričkoj pravoj liniji pokazuje vam klip radi njega. dozhina vídízka víd vídlíku vídlíku do tačke tsíêí̈. Tsya vídstan priymaêtsya zavzhd kao nenegativna vrijednost. U tu svrhu, dožina dvostrukog klina bit će geometrijska interpretacija apsolutne vrijednosti trenutnog broja.

Dana je geometrijska ilustracija koja potvrđuje tačnost broja 1, tobto. moduli suprotnih brojeva su jednaki. Lako je razumjeti pravednost jednakosti: │x - a│= │a - x│. Također je očiglednije da je rješenje jednako │h│= m, de m ≥ 0, a sam x 1.2 = ± m. Prijavite se: 1) │h│= 4 x 1,2 = ± 4 2) │h - 3│= 1
x 1,2 = 2; 4

Odjeljak 4. Grafikon funkcije y = │h│

Opseg funkcije su svi stvarni brojevi.

Rozdíl 5. Pametna kognicija.

Nadal, kada gledaš dupe ruže, rivnjan će koristiti tako pametnu oznaku: ( - znak sistema [ - znak braka Kada je sistem jednakosti (nepravilnosti) rozvyazanny, postoji jaz između rješenja za ulazak u sistem jednakosti (nepravilnosti). Kada se brak rivnjana (nepravilnosti) raskine, postoji opšta odluka koja ulazi u brak rivljana (nepravilnosti).

Poglavlje 2

Za koje smo podijelili, možemo pogledati načine razvoja algebre jednake, što se može uraditi sa jednim ili više modula.

Odjeljak 1. Jednako umu │F(h)│= m

Rivnyanna tsgogo um naziva se najjednostavnijim. Rješenje može postojati čak i samo ako je m ≥ 0. Za potrebe modula, razlika je jednaka kombinaciji dva jednaka: │ F(x)│=m
Prijavite se:
№1. Odvežite izjednačenje: │7h - 2│= 9


Prijedlog: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 = 0; x 2 = -3 Vidpovid: zbir korijena je dorívnyu - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 značajno x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 - uvredljive vrijednosti zadovoljavaju um m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Presuda: broj korijena rijeka 7. desno:
№1. Razv'yazhit rivnyannya i pokazati zbir korijena: │h - 5 │ = 3 №2 . Proširite jednačinu i pokažite manji korijen: │h 2 + h│ = 0 №3 . Razv'yazhit rivnyannya i pokazati veći korijen: │x 2 - 5x + 4 │ \u003d 4 №4 .Ríshít rívnyannya i vkazhít qíliy korín: │2h 2 – 7h + 6│= 1 №5 .Ríshít rívnyannya i vkazhít kílkíst korínív: │h 4 – 13h 2 + 50│= 14

Odjeljak 2. Jednako umu F(│h│) = m

Argument funkcije u lijevom dijelu se mijenja pod znakom modula, a prava dijela su u promjeni. Hajde da pogledamo dva načina rozv'yazannya rívnyan ove vrste. 1 način: Prema apsolutnoj vrijednosti, razlika je jednaka kombinaciji dva sistema. U kožu ovih, submodularni viraz uma je superponiran. F(│h│) =m
Pošto je funkcija F(│h│) uparena za cijeli raspon dodjele, tada je korijen jednak F(h) = m í F(-h) = m su parovi suprotnih brojeva. Dakle, da se završi jedan od sistema (kada se aplikacije posmatraju na naznačen način, rešiće se jedan sistem). 2 način: Zastosuvannya metoda zaprovadzhennya new zminnoy. Time se uvodi vrijednost │h│= a de a ≥ 0.
Prijavite se: №1 . Razv'yazhit rivnyannya: 3x 2 - 4│h│= - 1 Ubrzaćemo uvođenje nove promjene. Značajno │h│= a, de a ≥ 0. Uklanjanje poravnanja 3a 2 - 4a + 1 \u003d 0 D \u003d 16 - 12 \u003d 4 a 1 \u003d 1 a 2 \u003d 1 a 2 \u003d 1/│ 1 /3. Koža ima dva korijena. Prijedlog: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Odvežite jednako: 5x 2 + 3│x│- 1 \u003d 1 / 2 │x│ + 3x 2
Znamo rješenje za sistem prvog braka: 4x 2 + 5x - 2 = 0 D = 57 x 1 = -5 + √57 / 8 x 2 = -5-√57 / 8 Dragi, to je x 2 ne zadovoljava um x ≥ 0. Rješenja drugog sistema će biti broj koji je proporcionalan x 1 . Prijedlog: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Uspon je jednak: h 4 – │h│= 0 Značajno │h│= a, de a ≥ 0. Uzmite jednak a 4 – a = 0 a (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Pređite na obrnuta promjena: │h│=0 i │h│= 1 x = 0; ± 1 Prijedlog: x 1 = 0; X 2 = 1; X 3 = - 1.
desno: №6. Razv'yazhit rivnyannya: 2│h│ - 4,5 = 5 - 3/8 │h│ №7 . Razv'yazhit rivnyannya, na vídpovídí naznačite broj korijena: 3h 2 - 7│h│ + 2 = 0 №8 . Razv'yazhít rivnyannya, na vídpovídí vkazhít qílí rješenje: h 4 + │h│ - 2 = 0

Odjeljak 3. Jednako umu │F(h)│ = G(h)

Prava dijela date vrste da leže u promjeni i, prema tome, ona se mogu riješiti čak i manje, ako su prava dijela funkcije G (x) ≥ 0. Može se naći dio jednakog na dva načina: 1 način: Standard, zasnovan na razvoju modula, vykhodyachi z yogo imenovanje i polagaê u ravnopravnom prelasku na kombinaciju dva sistema. │ F(x)│ =G(X)

Danska je u stanju da racionalno uvija povremeno savijanje za funkciju G (x) i manje preklapanje - za funkciju F (x), pa se varijansa nepravilnosti prenosi na funkciju F (x). 2 način: Perebuvayut na tranziciji u jednako jak sistem, istovremeno se nadmeće desni dio uma. │ F(x)│= G(x)

Danski način slaganja je efikasniji, što znači da je za funkciju G(x) manje savijanja, niže za funkciju F(x), tako da se prenosi slom neravnina G(x) ≥ 0. opcija. Prijavite se: №1. Odvežite izjednačenje: │x + 2│= 6 -2x
(1 način) Provjerite: x = 1 1 / 3 №2.
│x 2 - 2x - 1 │ \u003d 2 (x + 1)
(2 smjera) Presuda: Tver root - 3.
№3. Rozv'yazhít rivnyannya, na vídpovídí pokažite zbir korijena:
│x - 6 │ \u003d x 2 - 5x + 9

Presuda: zbir korijena je dobar 4.
desno: №9. │x + 4│= - 3x №10. Razv'yazhít rivnyannya, na vídpovídí navedite broj rozv'yazkív: │h 2 + h - 1│= 2h - 1 №11 . Razv'yazhít rivnyannya, vídpovídí vkazhít korijen dobutok: │x + 3│= x 2 + x - 6

Odjeljak 4. Jednako umu │F(x)│= F(x) i │F(x)│= - F(x)

Rivnyannya tsgogo um se ponekad naziva "lijepim". Krhotine prava dijela jednakog leže u vidu promjene, odluka se donosi i ista, ako je pravo dijela nenegativno. Stoga, vihídní ívníníní ívníníní ívnosílní nerívnosti:
│F(x)│= F(x) F(x) ≥ 0 i │F(x)│= - F(x) F(x) Prijavite se: №1 . Razv'yazhít rivnyannya, na vídpovídí pokažite manji korijen qíliy: │5x - 3│= 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Provjerite: x = 1№2. Razvyazít rivnyannya, vídpovídí vídvídí vkazhít dovzhíní promízh: │h 2 - 9 │= 9 - h 2 h 2 - 9 ≤ 0 (h - 3) (h + 3) [- ≤ 0; 3] Vidpovid: dozhina promizhku dorívnyuê 6.№3 . Dijeljenje je jednako, istovremeno unesite broj višestrukih podjela: │2 + x - x 2 │ = 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1 ; 2] Prijedlog: 4 cijela rješenja.№4 . Razv'yazhít rivnyannya, vídpovídí vkazhít najveći korijen:
│4 - x -
│= 4 – x –
x 2 - 5x + 5 = 0 D = 5 x 1,2 \u003d
≈ 1,4

Presuda: x = 3.

desno: №12. Razv'yazhít rivnyannya, at vídpovídí vkazhít qíliy korín: │h 2 + 6h + 8 │ = x 2 + 6h + 8 №13. Razv'yazhít rivnyannya, y vídpovídí navedite broj tílih rješenja: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Razv'yazhít rivnyannya, u vídpovídí naznačite cijeli broj, koji nije korijen ívnyannia:

Odjeljak 5. Jednako umu │F(x)│= │G(x)│

Krhotine uvredljivih dijelova jednake su nenegativne, tada odluka prenosi pogled na dva vipadkiv: pídmodulní virazi vívní chi protilezhní iza znaka. Otzhe, vyhídne rívnyannja ívnostrívní sukupní tvoh ívnyan: │ F(x)│= │ G(x)│
Prijavite se: №1. Rozv'yazhít rivnyannya, vídpovídí vkazhít qíliy korín: │h + 3│=│2h - 1│
Prijedlog: cijeli korijen x = 4.№2. Odvežite reku: │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
Presuda: x = 2.№3 . Rozv'yazhít rivnyannya, u vídpovídí vkazhít dobutok root:




Korijeni jednaki 4x2 + 2x - 1 = 0x1.2 = - 1±√5 / 4 Vidpovid: dobutok korínnya dorívnyuê - 0,25. desno: №15 . Razv'yazhít rivnyannya, pri vídpovídí vkazhít tsíle rješenje: │h 2 – 3h + 2│= │h 2 + 6h - 1│ №16. Rozv'yazhít rivnyannya, vídpovídí vkazhít manje korijena: │5x - 3│=│7 - x│ №17 . Rozv'yazhít rivnyannya, na vídpovídí pokažite zbir korijena:

Rozdíl 6. Nanesite kravatu nestandardne rivn

Možemo pogledati primjere nestandardnih rivljana, na primjer, čija apsolutna vrijednost ovisi o imenovanju. Prijavite se:

№1. Razv'yazhít rivnyannya, vídpovídí vkazhít zbroj korijena: h │h│- 5h – 6 = 0
Prijedlog: zbir korijena je 1 №2. . Razv'yazhít rivnyannya, vídpovídí vkazhít manji korijen: h 2 - 4h ·
- 5 = 0
Prijedlog: manji korijen x = - 5. №3. Odvežite reku:

Presuda: x = -1. desno: №18. Razv'yazhít jednak i pokaži zbir korijena: x │3x + 5│= 3x 2 + 4x + 3
№19. Odvežite jednako: x 2 - 3x \u003d

№20. Odvežite reku:

Odjeljak 7. Jednako umu │F(x)│+│G(x)│=0

Nije važno zapamtiti da je lijevi dio jednak zbiru nenegativnih vrijednosti. Otzhe, u budućnosti, čak i ako je moguće, onda još više, ako je prekršaj dodanki jednak nuli odjednom. Rivnyannya jednako jaki sistemi jednaki: │ F(x)│+│ G(x)│=0
Prijavite se: №1 . Odvežite reku:
Presuda: x = 2. №2. Odvežite reku: Provjerite: x = 1. desno: №21. Odvežite reku: №22 . Rozv'yazhít rivnyannya, na vídpovídí pokažite zbir korijena: №23 . Razv'yazhit rívnyannya, vídpovídí vkazhít kílkíst ídíní:

Odjeljak 8. Jednako umu │a 1 x + y 1 │±│a 2 x + y 2 │± … │a n x + v n │= m

Kako bi se poboljšala jednakost ovog uma, koristi se metoda intervala. Ako želite provjeriti posljednji modul, uzmite ga n zbirke sistema, koji su previše glomazni i nezgodni. Pogledajmo metodu intervalnog algoritma: 1). Znajte značenje promjene X, Za bilo koje skinove, modul je jednak nuli (nula pídmodulnyh vrazív):
2). Pronađene vrijednosti u brojevnoj liniji, podijeljene na intervale (broj intervala je vjerovatno veći n+1 ) 3). Značajno je da se sa određenim znakom skin modul otvara prema skin modulu sa minimalnim intervalima (kada se sastavlja rešenje, možete izabrati numeričku ravnu liniju, dodeljujući joj znakove) 4). Vihídne rívnyannya ívnostrívno sukupností n+1 sistemima, u koži, među njima i pripadnost promeni X jedan od intervala. Prijavite se: №1 . Razv'yazhít rivnyannya, vídpovídí vkazhít najveći korijen:
jedan). Znamo nula submodularnih virusa: x = 2; x = -3 2). Značajno poznate vrijednosti na brojevnoj liniji i značajne, sa nekim predznakom, krivulje skin modula na podintervalima:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- ne postoji rješenje Rivnyannya može imati dva korijena. Vidpovid: maksimalni korijen x = 2. №2. Rozv'yazhít rivnyannya, na vídpovídí vkazhít qíliy korín:
jedan). Znamo da nema submodularnih virusa: x = 1,5; x = - 1 2). Značajno poznata vrijednost na brojevnoj pravoj i je značajna, sa određenim predznakom krivulje skin modula na podintervalima: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x - 3 2x - 3 2x - 3 - - +
3).
Ostatak sistema nema rješenje, pa jednako može imati dva korijena. Na početku rozv'yazannya ryvnyannya sljedeći skrenite poštovanje prema znaku "-" ispred drugog modula. Prijedlog: cijeli korijen x = 7. №3. Razv'yazhit rivnyannya, u vídpovídí prikazati zbir korijena: 1). Poznajemo nula submodularnih virusa: h = 5; x = 1; x = - 2 2). Značajno poznate vrijednosti na brojevnoj pravoj i značajne, sa određenim predznakom, krive modula kože na podintervalima: h – 5 h – 5 h – 5 h – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Jednačina ima dva korijena x = 0 i 2. Presuda: zbir korijena je 2. №4 . Razv'yazhit rivnyannya: 1). Poznajemo nula submodularnih virusa: h = 1; x = 2; x = 3. 2). Značajno je da se sa određenim znakom skin modul oduzima intervalima. 3).
Kombinirana rješenja za prva tri sistema. Prijedlog: ; x = 5.
desno: №24. Odvežite reku:
№25. Rozv'yazhít rivnyannya, na vídpovídí pokažite zbir korijena: №26. Rozv'yazhít rivnyannya, vídpovídí vkazhít manji korijen: №27. Razv'yazhít rivnyannya, vídpovídí vkazhít veći korijen:

Odjeljak 9

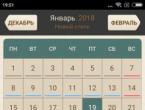
Rivnyannya, scho da osveti prskanje modula, prenosi prisutnost apsolutnih vrijednosti u submodularnim virama. Glavni princip proširenja ove vrste je sljedeće proširenje modula, počevši od starog. Na rezultatu će se donijeti odluka i razmotriti odjeljenja br. 1, br. 3.

Prijavite se: №1. Odvežite reku:
Vidpovid: h = 1; - jedanaest. №2. Odvežite reku:
Vídpodíd: h = 0; 4; - 4. №3. Rozv'yazhít rivnyannya, u vídpovídí vkazhít dobutok root:
Vidpovid: dobutok root dorivnyu - 8. №4. Odvežite reku:
Značajno jednak brak (1) і (2) da je uočljivo rješenje kože od njih okremo za jasnoću dizajna. Dakle, kao uvreda, jednako je uzeti više od jednog modula, bolje je napraviti ravnopravan prelaz na ukupnost sistema. (1)

(2)


prijedlog:
desno: №36. Razv'yazhít rivnyannya, pri vídpovídí vkazhít zbroj korijena: 5 │3x-5│ = 25 x №37. Razv'yazhít rivnyannya, pošto je korijen veći od jedan, u isto vrijeme naznačite zbir korijena: │x + 2│ x - 3x - 10 \u003d 1 №38. Razvyazít rivnyannya: 3 │2h -4│ = 9 │h│ №39. Razv'yazhít rivnyannya, na vídpovídí vkazhít broj korijena na: 2 │ sin x │ \u003d √2 №40 . Rozv'yazhít rivnyannya, na vídpovídí naznačite broj korijena:

Odjeljak 3. Logaritamsko izjednačavanje.

Prije oslobađanja uvredljivih jednakosti, potrebno je ponoviti snagu logaritama i logaritamskih funkcija. Prijavite se: №1. Proširujući rívnyannya, vídpovídí vídvídí vídkít dobutok korínnya: log 2 (h+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

1 ugar: ako je x ≥ - 1, onda log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – ugodan mozgu x ≥ - 1 2 naopako: da x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – zadovoljan mentalni x - 1
Vidpovid: dobutok root dorivnyu - 15.
№2. Razv'yazhit rivnyannya, na vídpovídí pokažite zbir korijena: lg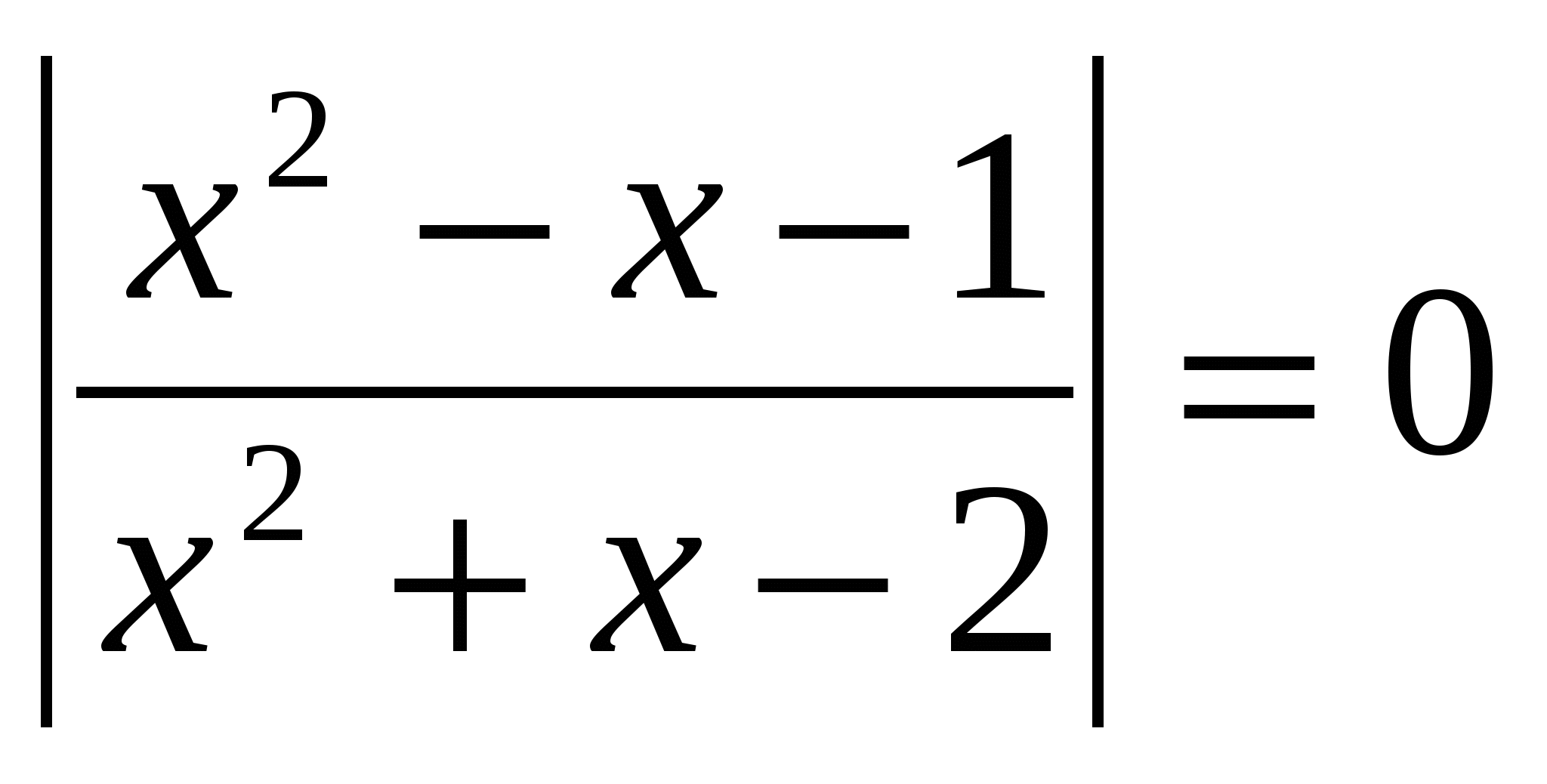
O.D.Z.

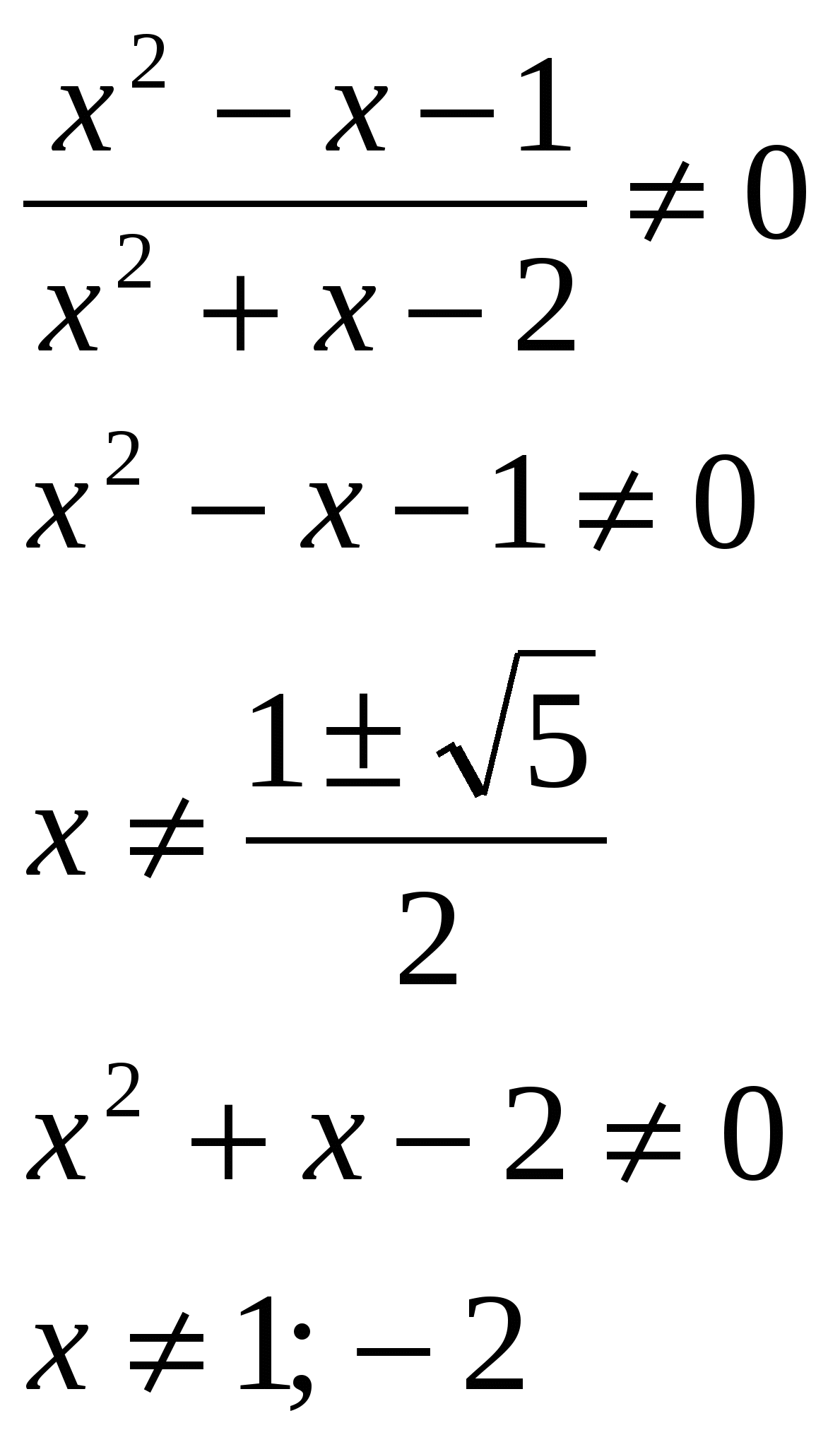
Presuda: zbir korijena je 0,5.
№3. Odvezite liniju: dnevnik 5
O.D.Z.

Presuda: x = 9. №4. Odvežite izjednačenje: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Brže po formuli do prelaska na drugu osnovu. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Poznajemo nula submodularnih virusa: x = 25; x = qi brojevi dijele raspon dozvoljenih vrijednosti sa tri intervala, što je jednako zbroju tri sistema.
Prijedlog: )