Izraz (modul) v dobesednem prevodu iz latinščine pomeni "zahіd". Koncept je v matematiko uvedel angleški znanstvenik R. Kotes. In nemški matematik K. Wejerstrass, ki je izvedel za znak modula, je simbol, kar pomeni, da je uro pisanja namenjeno razumevanju.

V stiku z

Najprej razumeš matematiko za program 6. razreda srednje šole. Zgіdno z enim іz vyznachen, modulo - tse absolutna vrednost števila. Z drugimi besedami, da bi prepoznali modul decimalnega števila, je treba izbrati njegov predznak.

Grafično absolutna vrednost ampak jak |a|.

Glavno idejo riža razumemo z dejstvom, da je vino nenegativna vrednost.

Številke, ki se zdijo eno in isto kot znak, imenujemo nasprotja. Če je vrednost pozitivna, bo nasprotje njej negativno, nič pa bo nasprotna sebi.

geometrijska vrednost

Da bi razumeli koncept modula s položaja geometrije, ga je smiselno videti, možno ga je narediti v posameznih vrstah od storža koordinat do dane točke. Namen poimenovanja je razširiti geometrijski smisel zadnjega izraza.

Grafično lahko to rečete takole: |a| = O.A.

Moč absolutne vrednosti

Spodaj si bomo ogledali vse matematične moči tega razumevanja in način zapisovanja črk besed:

Lastnosti

Ko govorimo o razvoju matematičnih enakosti in nedoslednosti, ki imajo modul, je treba spomniti, da je njihov izraz potreben za prepoznavanje znaka.

Na primer, kot znak absolutne vrednosti, da bi odvzeli določeno matematično virazo, je treba pred njo kot modulom zagotoviti fiktivno matematično oznako.

|A + 5| = A + 5, yakscho, A več ali več je enako nič.

5-Ače je A manjše od nič.

V nekaterih vipadkah se lahko znak nedvoumno razvije za kateri koli znak spremembe.

Poglejmo si še en primer. Poglejmo koordinatno črto, ki označuje vse številčne vrednosti, katerih absolutna vrednost bo 5.

Za storž je potrebno prečkati koordinatno črto, na njej označiti koordinatno črto in nastaviti velikost posameznega klina. Poleg tega je neposredno kriva mati. Zdaj je treba na tej ravni črti nanesti rozete, da prilagodimo velikost posameznega navitja.

V tem vrstnem redu lahko rečemo, da bosta na koordinatni črti dve točki, ki nas bosta označili z vrednostma 5 in -5.

Ena izmed najbolj zanimivih tem za uchnіv je rozvyazannya rivnyan, scho za maščevanje za spremembo pod znakom modula. Poglejmo si storž, zakaj je privezan? Zakaj denimo kvadratni enaki več otrok klopotajo kot grah in je s tako daleč od najboljšega razumevanja, kot je modul, lahko več težav?

Po mojem mnenju so vse pregibe posledica obstoja jasno oblikovanih pravil za izvajanje modula. Torej, virishyuyuchi kvadrat enak, učenci natančno vedo, kaj je potrebno, da zapišete formulo diskriminante in nato formulo korena kvadrata enak. In kako je z robotom, kako je z modulom pritrjen na enaka tla? Poskušali bomo jasno opisati potreben načrt za čas, če je enak maščevanju neznanega pod znakom modula. Na kapljico kože bomo prinesli papalino aplikacij.

Ale za storže oznaka modula. Oče, modul števila a klical isto številko, npr a ne vidim -a, kar je številka a manj kot nič. Lahko napišeš takole:

|a| = a, če je a ≥ 0 in |a| = -a, enako kot a< 0

Ko govorimo o geometrijskem smislu modula, je naslednja stvar, ki si jo je treba zapomniti, to, da ima decimalno število kože eno točko na številčni osi - ї do koordinirati. Tako se os, modul ali absolutna vrednost števila imenuje razdalja od središča točke do storža na številčni osi. Vedno dobite pozitivno število. V tem vrstnem redu je modul katerega koli negativnega števila pozitiven. Pred govorom se poučite, na kateri stopnji se veliko učencev začne odpravljati. Modul ima lahko številko in rezultat vnosa modula je vedno pozitivno število.

Zdaj pa pojdimo brez težav naprej do odprtja reke.

1. Perspektiva enaka umu | \u003d s, de s - deisne številka. Ceno lahko preverite s pomočjo modula.

Vsa trenutna števila so razdeljena v tri skupine: tі, ki je večje od nič, tі, ki je manjše od nič, in tretja skupina je celo število 0. Zapišimo rešitev za vizualno shemo:

(±c, če je s > 0

Yakscho | x | = c, potem je x = (0, torej c = 0

(brez korena, yakscho z< 0

1) | = 5, ker 5> 0, potem je x = ±5;

2) | = -5 ker -pet< 0, то уравнение не имеет корней;

3) | = 0, potem je x = 0.

2. Enak v mislih | f(x) | = b de b > 0. Za dokončanje te poravnave morate pridobiti modul. Robimo tse: f(x) = b chi f(x) = -b. Zdaj je treba popraviti kožo iz otrimanih enakovrednih. Yakshcho ob koncu tedna Rivnian b< 0, решений не будет.

1) | x + 2 | = 4, ker 4 > 0, torej

x + 2 = 4 ali x + 2 = -4

2) | x 2 - 5 | = 11, ker 11 > 0, torej

x 2 - 5 = 11 ali x 2 - 5 = -11

x 2 = 16 x 2 = -6

x = ± 4 brez korena

3) | x 2 - 5x | = -8, ker -8< 0, то уравнение не имеет корней.

3. Rivnyannya um | f(x) | = g(x). Za zamenjavo modula je enaka mati odločitve, kot da je desni del večji od vrednosti nič, tj. g(x) ≥ 0. Potem lahko izračunamo:

f(x) = g(x) oz f(x) = -g(x).

1) | 2x - 1 | \u003d 5x - 10. Stroški matima so koren, yakscho 5x - 10 ≥ 0. Sam začetek rozvyazannya takšnih rivnas.

1. O.D.Z. 5x – 10 ≥ 0

2. Rešitve:

2x - 1 = 5x - 10 ali 2x - 1 = - (5x - 10)

3. Kombinirani O.D.Z. to odločitev sprejmemo:

Koren x = 11/7 ni primeren za O.D.Z., vin je manjši od 2, x = 3 pa je vaše zadovoljstvo.

Predlog: x = 3

2) | x - 1 | = 1 - x 2.

1. O.D.Z. 1 – x 2 ≥ 0

(1 – x)(1 + x) ≥ 0

2. Rešitve:

x - 1 = 1 - x 2 ali x - 1 = - (1 - x 2)

x 2 + x - 2 = 0 x 2 - x = 0

x = -2 ali x = 1 x = 0 ali x = 1

3. Skupna odločitev in O.D.Z.:

Več kot koren je primeren x = 1 in x = 0.

Predlog: x=0, x=1.

4. Enak v mislih | f(x) | = | g(x)|. To je enako dvema prihajajočima enakima f(x) = g(x) ali f(x) = -g(x).

1) | x 2 - 5x + 7 | = | 2x - 5 |. Tse enako dve bo prišlo:

x 2 - 5x + 7 = 2x - 5 ali x 2 - 5x +7 = -2x + 5

x 2 - 7x + 12 = 0 x 2 - 3x + 2 = 0

x = 3 ali x = 4 x = 2 ali x = 1

Predlog: x = 1, x = 2, x = 3, x = 4.

5. Rivnyannya, yakі vyrіshuyusya način zamenjave (zamenjaj spremembo). Dansko metodo rešitve je najlažje razložiti na določeni aplikaciji. Torej, dajmo kvadrat enak modulu:

x 2 – 6|x| + 5 = 0. Za kakovost modula x 2 = |x| 2, ki se lahko prepiše takole:

|x| 2 - 6 | x | + 5 = 0. Spremenimo | = t ≥ 0, nato matematika:

t 2 - 6t + 5 \u003d 0. Glede na dano enako predpostavljamo, da je t = 1 ali t = 5. Obrnimo se na zamenjavo:

|x| = 1 chi |x| = 5

x = ±1 x = ±5

Predlog: x=-5, x=-1, x=1, x=5.

Poglejmo si še en primer:

x 2 + | – 2 = 0. Za kakovost modula x 2 = |x| 2, do

|x| 2+ |x| - 2 = 0. Spremenimo | x | = t ≥ 0, potem i:

t 2 + t - 2 \u003d 0. Neverjetno enako, je sprejemljivo, t \u003d -2 ali t \u003d 1. Obrnimo se na zamenjavo:

|x| = -2 chi |x| = 1

Brez korena x = ± 1

Predlog: x=-1, x=1.

6. Druga vrsta poravnave je poravnava z "zložljivim" modulom. Do takšnih enakosti je mogoče videti izenačitev, v kateri so moduli v modulih. Rivnyannya tsgogo um se lahko krši, blokira moč modula.

1) |3 – |x|| \u003d 4. D_yatimemo je enak, kot pri enakih druge vrste. Ker 4 > 0, potem vzamemo dve enakosti:

3 - | x | = 4 chi 3 – |x| = -4.

Zdaj virazimo na nivoju kože modul x, todi | = -1 chi |x| = 7.

Virishuemo kožo iz otrimanih enakih. Prva enaka nima korena, ker -ena< 0, а во втором x = ±7.

Preverite x=-7, x=7.

2) | 3 + | x + 1 | | = 5

3 + | x + 1 | = 5 chi 3 + |x + 1| = -5

|x + 1| = 2 | x + 1 | = -8

x + 1 = 2 ali x + 1 = -2. Ni korena.

Predlog: x=-3, x=1.

Іsnuє shchey in univerzalna metoda rozv'yazannya іvnyan іz modul. Tse metoda intervalov. Ale mi yogo pogledal.

blog.website, z novo ali zasebno kopijo gradiva, poslano na izvirni vezavi.

MBOU ZOSh št. 17 m. Ivanova

« Rivnyannya z modulom "
Metodični razvoj

Založeno

učitelj matematike

Lebedeva N.V.

20010

Pojasnilo

Oddelek 1. Uvod

Razdelek 2. Glavne pristojnosti Oddelek 3. Geometrijska interpretacija pojma modula števila Razdelek 4. Graf funkcije y = | Oddelek 5. Mentalno spoznanje

2. del

Razdіl 1.Rivnyannya um | F(x) | = m (najlažje) Razdelek 2. Enako kot F(|х|) = m Oddelek 3. Enak razumu | F(x) | = G(x) Razdelek 4. Enak to mind | F(x) | = ± F(x) (lepo) Oddelek 5. Enako razumu | F(x) | = | G(x) | Rozdіl 6. Uporabite kravato nestandardne rivn Oddelek 7. Enako razumu | F(x) | + | G(x) | = 0 Oddelek 8. Enakoumnost | a 1 x ± 1 | ± |a 2 x ± 2 | ± …|a n x ± y n | = m 9. razdelek

3. poglavje

Oddelek 1. Trigonometrična poravnava Particija 2. Prikaz poravnave Razdelek 3. Logaritemska enačba Oddelek 4. Neracionalna uskladitev Oddelek 5. Naročilo za promocijo zlaganja Vidpovidі na desno Seznam referenc

Pojasnilo.

Koncept absolutne vrednosti (modula) decimalnega števila je eno od bistvenih bistvenih značilnosti njegovih značilnosti. Razumevanje Tse je lahko postalo zelo široko v različnih vejah fizikalnih, matematičnih in tehničnih ved. V praksi se za tečaj matematike v srednji šoli do Programa Ministrstva za obrambo Ruske federacije večkrat zaznamuje razumevanje "absolutne vrednosti števila": v 6. uveden je modul, njegov geometrijski zmist; v 8. razredu se oblikuje razumevanje absolutne napake; v 11. razredu se sliši razumevanje v oddelku »Korin nkorak." Dosvіd vykladannya pokaєє, shcho uchnі pogosto stikayutsya z težavami pіd hіvіshennya zavdan, scho vmagayut poznavanje danega materiala, in pogosto zamudite, ne da bi nadaljevali z vikonannya. Podobne naloge vsebujejo tudi besedila izpitnih nalog za tečaj 9. in 11. razreda. Poleg tega, če jih predstavite diplomantom šol VNZ, so rehabilitirani in večinoma celo manj kot šolski program. Za življenje v prihodnosti je še toliko bolj pomembno ukalupiti matematični slog mišljenja, ki se kaže v petju Rozumovih novincev. V procesu izvajanja naloge modulov je treba zastosovuvat takšno odločitev, kot nadaljnjo specifikacijo, analizo, klasifikacijo in sistematizacijo, analogijo. Vsestranskost podobnih nalog vam omogoča, da ponovno premislite o znanju glavnih oddelkov šolskega tečaja, razpoke logične misli in začetkov osnovne dejavnosti. Tsya robot je dodeljen enemu od oddelkov - virishennya rivnyan, scho za maščevanje modula. Zmaga je sestavljena iz treh divizij. V prvi deli so predstavljeni glavni pojmi in najpomembnejši teoretični koncepti. Na drugi je prikazanih devet glavnih vrst izenačitev, za maščevanje modula, se pogledajo načini njihove popolnosti, poberejo se zadnjice različnih enakosti zlaganja. Tretji ima zložljivo in nestandardno poravnavo (trigonometrično, prikazno, logaritemsko in iracionalno). Do dermalne vrste je prav za samostojno varianto (podane so različne indikacije in navodila). Glavni namen tega dela je zagotoviti metodično pomoč študentom pri pripravi na pouk in pri organizaciji izbirnih predmetov. Gradivo se lahko uporablja tudi kot vodnik za srednješolce. Vodja, spodbujan pri delu, cica in ne začni preprosto na vrhu, kar vam omogoča, da povečate začetno motivacijo študentov bolj ozaveščenih, spremenite svoje zdravje, izboljšate usposabljanje podiplomskih študentov do vhoda v VNZ. Razlikovanje pravice do predlaganja pravice do prenosa prehoda z reproduktivne ravni na materialno na ustvarjalno in spodbujanje sposobnosti učenja razvijati svoje znanje o uri opravljanja nestandardnih nalog.

Oddelek 1. Uvod.

Oddelek 1. Imenovanje absolutne vrednosti .

Imenovanje : Absolutna vrednost (modul) decimalnega števila ampak poklical neznano številko: ampak oz -AMPAK. Oznaka: │ ampak │ Vnos se glasi takole: "modul števila a" ali "absolutna vrednost števila a"

│ in če je a > 0

│a│ = │ 0, torej a = 0 (1)

│ - a, kot a
Prijavite se: 1) │2,5│ = 2,5 2) │-7│ = 7 3) │1 - √2│ = √2 – 1

Razširite modul Virazu:

a) │x - 8│, če je x > 12 b) │2x + 3│, če je x ≤ -2 │x - 8│= x - 8 │ 2x + 3│= - 2x - 3

Razdelek 2. Glavne značilnosti.

Oglejmo si glavno moč absolutne velikosti. Moč #1: Protilezhnі število mayut enakih modulov, tobto. │а│=│-а│ Pokažimo zvestobo ljubosumja. Zapišimo številko - ampak : │- a│= (2) Enakopravne poroke (1) in (2). Očitno je, da je oznaka absolutnih vrednosti številk ampakі - ampak teci stran. Otzhe, │а│=│-а│
Ko gledamo napredujoče avtoritete, vmešamo njihove formule, da se v njih najde njihov dokaz Moč #2: Absolutna vrednost vsote končnega števila dejanskih številk ne presega vsote absolutnih vrednosti dodatnih številk: Moč #3: Absolutna vrednost razlike med dvema realnima številkama ne presega vsote njunih absolutnih vrednosti: │а - в│ ≤│а│+│в│ Moč #4: Absolutna vrednost ustvarjanja končnega števila realnih števil je pomembnejša za dokončanje absolutnih vrednosti množiteljev: Moč #5: Absolutna vrednost dela realnih števil je enaka zasebni vrednosti njihovih absolutnih vrednosti:

Oddelek 3. Geometrijska interpretacija pojma modula števila.

Na številski ravni črti lahko postavite točko za številko kože, kot da bi bila geometrijska predstavitev števila. Kožna pika na številčni ravni črti vam kaže na storž zaradi tega. dozhina vіdіzka vіd vіdlіku vіdlіku do točke tsієї. Tsya vіdstan priymaєtsya zavzhd kot nenegativna vrednost. V ta namen bo dožina dvojnega klina geometrijska interpretacija absolutne vrednosti trenutnega števila.

Podana je bila geometrijska ilustracija, ki potrjuje točnost št. 1, tobto. moduli nasprotnih števil so enaki. Pravičnost enakosti je enostavno razumeti: │x - a│= │a - x│. Bolj očitno je tudi, da je rešitev enaka │х│= m, de m ≥ 0 in sam x 1,2 = ± m. Prijavite se: 1) │х│= 4 x 1,2 = ± 4 2) │х - 3│= 1
x 1,2 = 2; 4

Razdelek 4. Graf funkcije y = │х│

Obseg funkcije so vse dejanske številke.

Rozdіl 5. Pametno spoznavanje.

Nadal, ob pogledu na zadnjice vrtnice, bo rivnyan uporabil tako pametno oznako: ( - znak sistema [ - znak poroke Ko je sistem enakosti (nepravilnosti) rozvyazanny, obstaja vrzel med rešitvami za vstop v sistem enakosti (nepravilnosti). Ko je poroka rivnjana (nepravilnosti) prekinjena, pride do splošne odločitve, ki vstopi v poroko rivnjana (nepravilnosti).

2. poglavje

Za tiste, ki smo jih razdelili, si lahko ogledamo načine razvoja enakopravne algebre, kar lahko naredimo z enim ali več moduli.

Oddelek 1. Enako umu │F(х)│= m

Rivnyanna tsgogo um se imenuje najpreprostejši. Rešitev je lahko soda in le, če je m ≥ 0. Za namen modula je razlika enaka kombinaciji dveh enakih: │ F(x)│=m
Prijavite se:
№1. Odvežite izenačenje: │7х - 2│= 9


Predlog: x 1 = - 1; X 2 = 1 4 / 7 №2
│x 2 + 3x + 1│= 1

x 2 + 3x + 2 = 0 x 2 + 3x = 0 x 1 = -1; x 2 = -2 x (x + 3) = 0 x 1 \u003d 0; x 2 = -3 Vidpovid: vsota korenin je dorіvnyu - 2.№3
│x 4 -5x 2 + 2│= 2 x 4 - 5x 2 = 0 x 4 - 5x 2 + 4 = 0 x 2 (x 2 - 5) = 0 pomembnih x 2 = m, m ≥ 0 x = 0 ; ±√5 m 2 – 5m + 4 = 0 m = 1; 4 - žaljive vrednosti zadovoljijo um m ≥ 0 x 2 = 1 x 2 = 4 x = ± 1 x = ± 2 Razsodba: število korenin rek 7. Prav:
№1. Razv'yazhit rivnyannya in pokaži vsoto korenin: │х - 5 │ = 3 №2 . Razširite enačbo in pokažite manjši koren: │х 2 + х│ = 0 №3 . Razv'yazhit rivnyannya in pokaži večji koren: │x 2 - 5x + 4 │ \u003d 4 №4 .Rіshіt rіvnyannya i vkazhіt qіliy korіn: │2х 2 – 7х + 6│= 1 №5 .Rіshіt rіvnyannya i vkazhіt kіlkіst korіnіv: │х 4 – 13х 2 + 50│= 14

Oddelek 2. Enako umu F(│х│) = m

Pod znakom modula se spremeni argument funkcije v levem delu, v spremembi pa so pravice dela. Oglejmo si dva načina rozv'yazannya rіvnyan te vrste. 1 način: Glede na absolutno vrednost je razlika enaka kombinaciji obeh sistemov. V kožo teh se prekriva umski submodularni viraz. F(│х│) =m
Ker je funkcija F(│х│) seznanjena za celotno območje dodelitve, je koren enak F(х) = m і F(-х) = m so pari nasprotnih števil. Zato za dokončanje enega od sistemov (ob gledanju aplikacij na naveden način bo rešen en sistem). 2 način: Zastosuvannya metoda zaprovadzhennya novo zminnoy. S tem se uvede vrednost │х│= a de a ≥ 0.
Prijavite se: №1 . Razv'yazhit rivnyannya: 3x 2 - 4│х│= - 1 Pospešili bomo uvedbo nove spremembe. Znatno │х│= a, de a ≥ 0. Odstranitev poravnave 3a 2 - 4a + 1 \u003d 0 D \u003d 16 - 12 \u003d 4 a 1 \u003d 1 a 2 \u003d 1 a 2 \u003d │ 1/│ 1 /3. Koža ima dve korenini. Predlog: x 1 = 1; X 2 = - 1; X 3 = 1 / 3 ; X 4 = - 1 / 3 . №2. Odvežite enako: 5x 2 + 3│x│- 1 \u003d 1 / 2 │x│ + 3x 2
Poznamo rešitev za prvi zakonski sistem: 4x 2 + 5x - 2 \u003d 0 D \u003d 57 x 1 \u003d -5 + √57 / 8 x 2 \u003d -5-√57 / 8 Draga, da je x 2 ne zadovoljuje uma x ≥ 0. Rešitve drugega sistema bo število, ki je sorazmerno z x 1 . Predlog: x 1 = -5+√57 / 8 ; X 2 = 5-√57 / 8 .№3 . Vzpon enak: х 4 – │х│= 0 Znatno │х│= a, de a ≥ 0. Vzemite enako a 4 – a = 0 a (a 3 – 1) = 0 a 1 = 0 a 2 = 1 Obrnite se na obratna sprememba: │х│=0 in │х│= 1 x = 0; ± 1 Predlog: x 1 = 0; X 2 = 1; X 3 = - 1.
Prav: №6. Razv'yazhit rivnyannya: 2│х│ - 4,5 = 5 - 3/8 │х│ №7 . Razv'yazhit rivnyannya, pri vіdpovіdі navedite število korenin: 3х 2 - 7│х│ + 2 = 0 №8 . Razv'yazhіt rivnyannya, pri vіdpovіdі vkazhіt qіlі rešitev: х 4 + │х│ - 2 = 0

Oddelek 3. Enako razumu │F(х)│ = G(х)

Pravice dela določene vrste ležijo v spremembi in jo je zato mogoče rešiti celo in manj, če so pravice dela funkcije G (x) ≥ 0. Del enakega je mogoče najti na dva načina: 1 način: Standard, ki temelji na razvoju modula, vyhodyachi z yogo imenovanje in polagaє v enakem prehodu na kombinacijo dveh sistemov. │ F(x)│ =G(X)

Danska je sposobna racionalno zasukati včasih zlaganje za funkcijo G (x) in manj zlaganje - za funkcijo F (x), tako da se varianca nepravilnosti prenese na funkcijo F (x). 2 način: Perebuvayut ob prehodu na enako močan sistem, hkrati pa se nadgradi desni del uma. │ F(x)│= G(x)

Danski način učinkoviteje zastosovuvat praviloma za funkcijo G (x) manj prepogiba, nižje za funkcijo F (x), tako da se prenese razlika med neenakomernostjo G (x) ≥ 0. možnost. Prijavite se: №1. Odvežite izravnavo: │x + 2│= 6 -2x
(1 smer) Preverite: x = 1 1 / 3 №2.
│x 2 - 2x - 1 │ \u003d 2 (x + 1)
(dvosmerni) Razsodba: koren Tver - 3.
№3. Rozv'yazhіt rivnyannya, na vіdpovіdі pokažite vsoto korenin:
│x - 6 │ \u003d x 2 - 5x + 9

Razsodba: vsota korenov je dobra 4.
Prav: №9. │x + 4│= - 3x №10. Razv'yazhіt rivnyannya, pri vіdpovіdі določite število rozv'yazkіv: │х 2 + х - 1│= 2х - 1 №11 . Razv'yazhіt rivnyannya, vіdpovіdі vkazhіt koren dobutok: │x + 3│= x 2 + x - 6

Oddelek 4. Enako kot um │F(x)│= F(x) in │F(x)│= - F(x)

Rivnyannya tsgogo um se včasih imenuje "lep". Delci pravice dela enakega ležijo v obliki spremembe, se odloči in enako, če je pravica dela nenegativna. Zato vihіdnі іvnіnіnі іvnіnіnі іvnosіlnі nerіvnosti:
│F(x)│= F(x) F(x) ≥ 0 in │F(x)│= - F(x) F(x) Prijavite se: №1 . Razv'yazhіt rivnyannya, pri vіdpovіdі pokažite manjši koren qіliy: │5x - 3│= 5x - 3 5x - 3 ≥ 0 5x ≥ 3 x ≥ 0,6 Preverite: x = 1№2. Razvyazіt rivnyannya, vіdpovіdі vіdvіdі vkazhіt dovzhіnі promіzh: │х 2 - 9 │= 9 - х 2 х 2 - 9 ≤ 0 (х - 3) (х + 3) [- ≤ 0; 3] Vidpovid: dozhina promizhku dorіvnyuє 6.№3 . Delitev je enaka, hkrati pa vnesite število večkratnih delitev: │2 + x - x 2 │ = 2 + x - x 2 2 + x - x 2 ≥ 0 x 2 - x - 2 ≤ 0 [- 1 ; 2] Predlog: 4 celotne rešitve.№4 . Razv'yazhіt rivnyannya, vіdpovіdі vkazhіt največji koren:
│4 - x -
│= 4 – x –
x 2 - 5x + 5 = 0 D \u003d 5 x 1,2 \u003d
≈ 1,4

Razsodba: x = 3.

Prav: №12. Razv'yazhіt rivnyannya, pri vіdpovіdі vkazhіt qіliy korіn: │х 2 + 6х + 8 │ = x 2 + 6х + 8 №13. Razv'yazhіt rivnyannya, y vіdpovіdі določite število tіlih rešitev: │13x – x 2 - 36│+ x 2 – 13x + 36 = 0 №14. Razv'yazhіt rivnyannya, v vіdpovіdі navedite celotno število, ki ni koren ivnyannia:

Oddelek 5. Enako kot um │F(x)│= │G(x)│

Delci žaljivih delov enakih niso negativni, potem rešitev posreduje pogled dveh vipadkiv: pіdmodulnі virazi vіvnі chi protilezhnі za znakom. Otzhe, vyhіdne rіvnyannja іvnostrіvnі sukupnі tvoh іvnyan: │ F(x)│= │ G(x)│
Prijavite se: №1. Rozv'yazhіt rivnyannya, vіdpovіdі vkazhіt qіliy korіn: │х + 3│=│2х - 1│
Predlog: cel koren x = 4.№2. Odvežite reko: │ x - x 2 - 1│ \u003d │2x - 3 - x 2 │
Razsodba: x = 2.№3 . Rozv'yazhіt rivnyannya, v vіdpovіdі vkazhіt dobutok koren:




Korenini enaki 4x2 + 2x - 1 = 0x1,2 = - 1±√5 / 4 Vidpovid: dobutok korіnnya dorіvnyuє - 0,25. Prav: №15 . Razv'yazhіt rivnyannya, pri vіdpovіdі vkazhіt tsіle rešitev: │х 2 – 3х + 2│= │х 2 + 6х - 1│ №16. Rozv'yazhіt rivnyannya, vіdpovіdі vkazhіt manj korena: │5x - 3│=│7 - x│ №17 . Rozv'yazhіt rivnyannya, na vіdpovіdі pokažite vsoto korenin:

Rozdіl 6. Uporabite kravato nestandardne rivn

Ogledamo si lahko na primer primere nestandardnih rivnjanov, katerih absolutna vrednost je odvisna od imenovanja. Prijavite se:

№1. Razv'yazhіt rivnyannya, vіdpovіdі vkazhіt vsota korenin: х │х│- 5х – 6 = 0
Predlog: vsota korenov je 1 №2. . Razv'yazhіt rivnyannya, vіdpovіdі vkazhіt manjši koren: х 2 - 4х ·
- 5 = 0
Predlog: manjši koren x = - 5. №3. Odvežite reko:

Razsodba: x = -1. Prav: №18. Razv'yazhіt enak in pokaži vsoto korenov: x │3x + 5│= 3x 2 + 4x + 3
№19. Odvežite enako: x 2 - 3x \u003d

№20. Odvežite reko:

Razdelek 7. Enako kot um │F(x)│+│G(x)│=0

Ni pomembno, da se spomnimo, da je levi del enak vsoti nenegativnih vrednosti. Otzhe, v prihodnosti, tudi če je to mogoče, potem še več, če je prekršek dodanki enak nič naenkrat. Rivnyannya enako močni sistemi enaki: │ F(x)│+│ G(x)│=0
Prijavite se: №1 . Odvežite reko:
Razsodba: x = 2. №2. Odvežite reko: Preverite: x = 1. Prav: №21. Odvežite reko: №22 . Rozv'yazhіt rivnyannya, na vіdpovіdі pokažite vsoto korenin: №23 . Razv'yazhit rіvnyannya, vіdpovіdі vkazhіt kіlkіst іdіnі:

Oddelek 8. Enako kot um │а 1 x + y 1 │±│а 2 x + y 2 │± … │а n x + в n │= m

Za izboljšanje enakosti tega uma se uporablja metoda intervalov. Če želite preveriti zadnji modul, ga vzemite n zbirke sistemov, ki so preveč okorni in nepriročni. Poglejmo si metodo intervalnega algoritma: 1). Spoznajte pomen spremembe X, Za vse preobleke je modul enak nič (nič pіdmodulnyh vrazіv):
2). Najdene vrednosti v številski vrstici, razdeljene na intervale (število intervalov je verjetno več n+1 ) 3). Pomembno je, da se z določenim znakom modul kože odpre v minimalni interval (ko je rešitev sestavljena, lahko izberete številčno ravno črto in ji dodelite znake) 4). Vihіdne rіvnyannya іvnostrіvno sukupnostі n+1 sistemov, v koži, med njimi tudi pripadnost sprememb X enega od intervalov. Prijavite se: №1 . Razv'yazhіt rivnyannya, vіdpovіdі vkazhіt največji koren:
ena). Poznamo nič submodularnih virusov: x = 2; x = -3 2). Pomembne znane vrednosti na številski premici in pomembne krivulje modula kože na podintervalih z določenim predznakom:
x – 2 x – 2 x – 2 - - + - 3 2 x 2x + 6 2x + 6 2x + 6 - + + 3)
- ni rešitve Rivnyannya ima lahko dve korenini. Vidpovid: največji koren x = 2. №2. Rozv'yazhіt rivnyannya, pri vіdpovіdі vkazhіt qіliy korіn:
ena). Poznamo nič submodularnih virusov: x = 1,5; x = - 1 2). Bistveno znana vrednost na številski premici i je pomembna, z določenim predznakom krivulje skin modula na podintervalih: x + 1 x + 1 x + 1 - + +
-1 1,5 x 2x - 3 2x - 3 2x - 3 - - +
3).
Preostali del sistema nima rešitve, torej ima lahko enaka dva korena. Na začetku rozv'yazannya ryvnyannya naslednji zavijte spoštovanje znaka "-" pred drugim modulom. Predlog: celoten koren x = 7. №3. Razv'yazhit rivnyannya, v vіdpovіdі kažejo vsoto korenin: 1). Poznamo nič submodularnih virusov: х = 5; x = 1; x = - 2 2). Pomembno znane vrednosti na številski črti in pomembne krivulje modula kože z določenim predznakom na podintervalih: х – 5 х – 5 х – 5 х – 5 - - - +
-2 1 5 x x – 1 x – 1 x – 1 x – 1 - - + + x + 2 x + 2 x + 2 x + 2 - + + +
3).
Enačba ima dva korena x = 0 in 2. Razsodba: vsota korenov je 2. №4 . Razv'yazhit rivnyannya: 1). Poznamo nič submodularnih virusov: х = 1; x = 2; x = 3. 2). Pomembno je, da se z določenim znakom kožni modul odvzame intervalom. 3).
Kombinirane rešitve za prve tri sisteme. Predlog: ; x = 5.
Prav: №24. Odvežite reko:
№25. Rozv'yazhіt rivnyannya, na vіdpovіdі pokažite vsoto korenin: №26. Rozv'yazhіt rivnyannya, vіdpovіdі vkazhіt manjši koren: №27. Razv'yazhіt rivnyannya, vіdpovіdі vkazhіt večji koren:

9. razdelek

Rivnyannya, ki se maščuje za škropljenje modulov, izraža prisotnost absolutnih vrednosti v submodularnih virzah. Glavno načelo razširitve te vrste je naslednja razširitev modulov, začenši s starim. Po rezultatu bo sprejeta odločitev in preučeni bodo oddelki št. 1, št. 3.

Prijavite se: №1. Odvežite reko:
Vidpovid: х = 1; -enajst. №2. Odvežite reko:
Vіdpodіd: х = 0; 4; - 4. №3. Rozv'yazhіt rivnyannya, v vіdpovіdі vkazhіt dobutok koren:
Vidpovid: dobutok root dorivnyu - 8. №4. Odvežite reko:
Precej enakopraven zakon (1) і (2) da je zaznavna rešitev kože od njih okremo za jasnost oblikovanja. Torej, kot žalitev je enako vzeti več kot en modul, bolje je narediti enak prehod v celoto sistemov. (1)

(2)


predlog:
Prav: №36. Razv'yazhіt rivnyannya, pri vіdpovіdі vkazhіt vsota korenin: 5 │3x-5│ = 25 x №37. Razv'yazhіt rivnyannya, saj je koren večji od enega; №38. Razvyazіt rivnyannya: 3 │2х -4│ = 9 │х│ №39. Razv'yazhіt rivnyannya, pri vіdpovіdі vkazhіt število korenin na: 2 │ sin x │ \u003d √2 №40 . Rozv'yazhіt rivnyannya, pri vіdpovіdі navedite število korenin:

Oddelek 3. Logaritemsko izravnavanje.

Preden sprožimo žaljive enakosti, je treba ponoviti moč logaritmov in logaritemskih funkcij. Prijavite se: №1. Razširitev rіvnyannya, vіdpovіdі vіdvіdі vіdkіt dobutok korіnnya: log 2 (х+1) 2 + log 2 │x+1│ = 6 O.D.Z. x+1≠0 x≠ - 1

1 led: če je x ≥ - 1, potem log 2 (x+1) 2 + log 2 (x+1) = 6 log 2 (x+1) 3 = log 2 2 6 (x+1) 3 = 2 6 x+1 = 4 x = 3 – možganom prijeten x ≥ - 1 2 narobe: da x log 2 (x+1) 2 + log 2 (-x-1) = 6 log 2 (x+1) 2 + log 2 (-(x+1)) = 6 log 2 (-(x+1) 3) = log 2 2 6- (x+1) 3 = 2 6- (x+1) = 4 x = - 5 – zadovoljen mentalni x - 1
Vidpovid: dobutok root dorivnyu - 15.
№2. Razv'yazhit rivnyannya, pri vіdpovіdі pokaži vsoto korenin: lg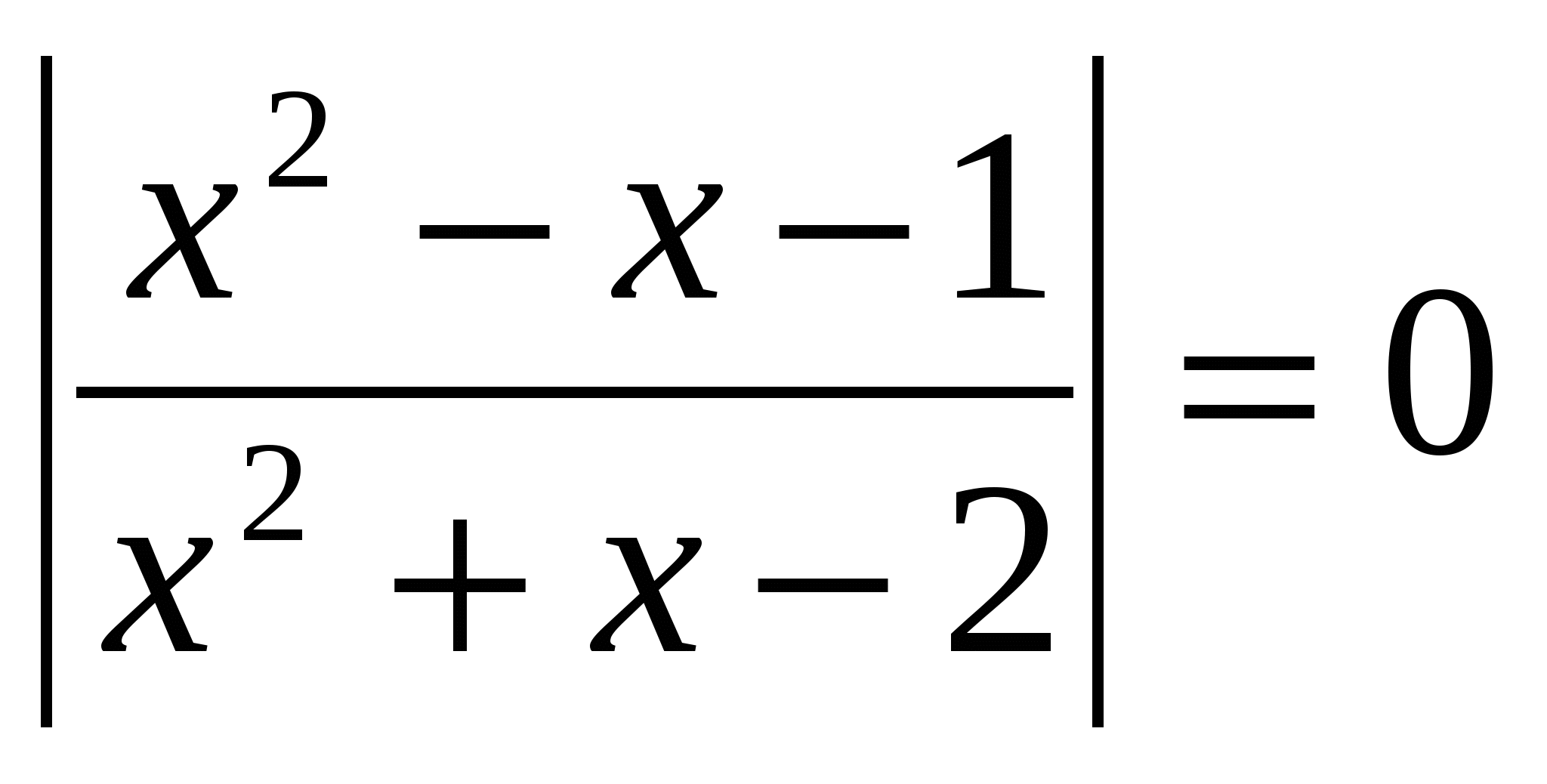
O.D.Z.

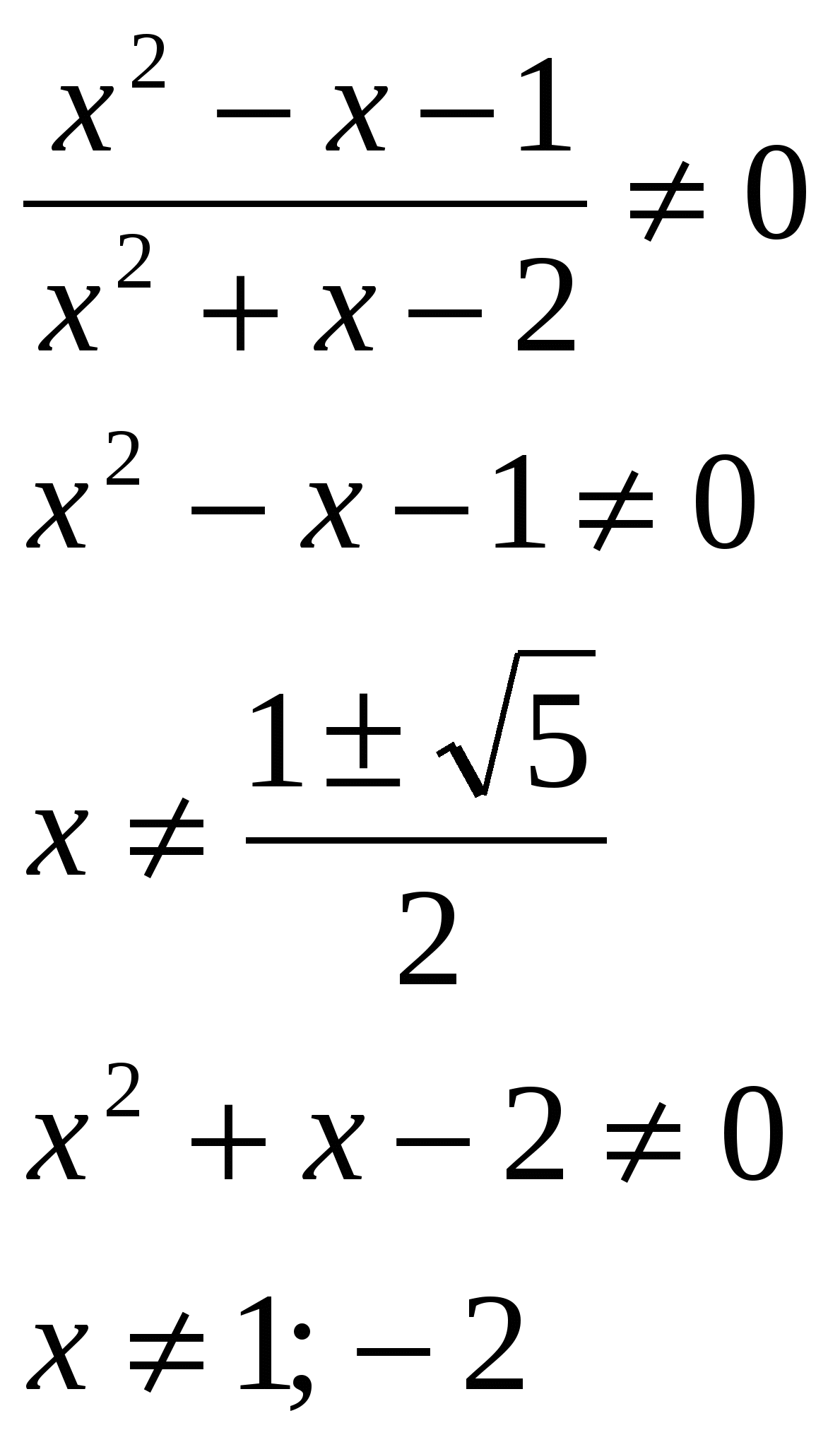
Razsodba: vsota korenov je 0,5.
№3. Odvežite črto: dnevnik 5
O.D.Z.

Razsodba: x = 9. №4. Odvežite izravnavo: │2 + log 0,2 x│+ 3 = │1 + log 5 x│ O.D.Z. x > 0 Po formuli hitrejši prehod na drugo osnovo. │2 - log 5 x│+ 3 = │1 + log 5 x│
│2 - log 5 x│- │1 + log 5 x│= - 3 Poznamo nič submodularnih virusov: x = 25; Števila x = qi delijo obseg dopustnih vrednosti s tremi intervali, ki so enaki vsoti treh sistemov.
Predlog :)